許多情況下,一組觀測值的取值很明顯是取決於另一組觀測值。
本次的案例中每個「個體」都有兩個觀測值。
一個觀測值是「原因變數」、「x 變數」、「預測變數」、「自變數」,
此變數的取值為實驗者的設定或選擇;
另一個觀測值是「效果變數」、「y 變數」、「應變數」,此變數的取值非實驗者設定。
有一系列方式可以判斷原因和效果之間的關係形式和強度,每個方法對變數及其關係的假定各有不同,
這裡考慮五種檢定: 線性回歸、Kendall 最佳配適線、羅吉斯回歸、第二型模式回歸和多項式回歸。
「標準」線性回歸
即第一型模式回歸,是生物學中常用的統計模式,也是最常被濫用的統計方法,因為常忽略它的假定。
線性回歸可判定兩個變數之間關係的形式和強度,很強大且有用。
如果想要用給定 x 值(自變數)來預測 y 值(應變數),就可運用。
此檢定是在判斷斜率是否為 0 (虛無假設 b=0),如果 p< 0.05 代表斜率和 0 有顯著差異,x 和 y 變數之間有關係。
線性回歸對資料有許多假定,包括 x 值沒有誤差;x 值是由實驗者選擇或指定; x 和 y 之間關係的最佳描述為一條直線 (y= bx); 不論 x 取值為何,y 的變異數均相等,以及不論 x 取值為何,y 均遵守常態分佈。
#Exmple: 研究實驗藥物的胃部吸收,試驗胃部的酸性程度是否會影響吸收。
uptake<- c(11.32,11.29,11.37,11.32,11.32,11.49,
11.31,11.22,11.40,11.31,11.36,11.52,
11.22,11.18,11.38,11.35,11.40,11.38,
11.23,11.21,11.37,11.32,11.35,11.49)
pH<- rep(seq(from=0.6, to= 1.6,by=0.2),times= 4)
drug<- data.frame(pH,uptake)
summary(lm(uptake~pH))
#lm()可執行簡單線性回歸,輸出結果給出lm()的使用模型,報告殘差分布狀況;殘差為各點和擬和直線的垂直距離。最好的情況為殘差的分布是對稱的,且中位數是0。輸出的截距為 X (pH)為 0 時 y (uptake)的取值 (11.12695),且和 0 有顯著差異。第二列給出關係的斜率 (0.19)和顯著性(0.000018)。這代表 pH 每增加 1,uptake 會增加 0.19,且此斜率和虛無假設的 0 有顯著差異。
R-squared 為 0.574,意謂反應變數(uptake)的變異數的 57%可被預測變數(pH)解釋。
Call:
lm(formula = uptake ~ pH)
Residuals:
Min 1Q Median 3Q Max
-0.10038 -0.04586 -0.00956 0.05619 0.08619
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 11.12695 0.04057 274.296 < 2e-16 ***
pH 0.19179 0.03522 5.446 1.8e-05 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.05893 on 22 degrees of freedom
Multiple R-squared: 0.5741, Adjusted R-squared: 0.5547
F-statistic: 29.65 on 1 and 22 DF, p-value: 1.804e-05
plot(pH,uptake)
abline(11.127,0.192) #以abline()畫出輸出結果的最佳擬和線
m<- lm(uptake~pH)
plot(m) #畫出一系列的資料與殘差圖
#Kendall最佳配適線 (Kendall robust line-fit method): 一種簡單的無母數統計方法,可代替一般回歸,計算方式很簡單,把(x,y)點的資料兩兩配對,並將其間的斜率算出來(5個資料點就有10個斜率,10個就有45個)。這些斜率的中位數被選為b的最佳估計值,並用這個斜率將每個資料的x取0,即可得到很多截距,在取這些截距的中位數為截距。該方法假定很少,只要求資料的尺度需有實際意義。
#羅吉斯回歸 (Logistic regression): 為回歸分析的一種特殊形式,限於應變數為組別形式時使用。此回歸法把應變數中兩種可能取值作羅吉斯轉換後,在對自變數做回歸。當比例為0或1時,此回歸法會顯得更有用。
#與線性回歸不同的是,此回歸的自變數尺度不需要實際意義。就算x軸只有兩個取值(有、沒有),依然可以執行羅吉斯回歸。它會將「效果」值做羅吉斯轉換。可以區別函數分析依樣當成分類的工具。
#Example: 虛無假設為「某植物病毒盛行率和遮陰狀況無關」。以光度計測量結果訂定七個遮陰水準。每個水準都逢積選取10株植物,並紀錄是否帶有病毒。
shade<- c(rep(1,times=10),rep(2,times=10),rep(3,times=10),rep(4,times=10),rep(5,times=10),rep(6,times=10),rep(7,times=10))
virus<- c(T,T,F,F,F,F,F,F,F,F,
T,T,T,T,F,F,F,F,F,F,
T,T,T,T,F,F,F,F,F,F,
T,T,T,T,F,F,F,F,F,F,
T,T,T,T,T,T,F,F,F,F,
T,T,T,T,T,T,F,F,F,F,
T,T,T,T,T,T,T,T,F,F)
summary(glm(virus~shade, binomial)) #使用glm()函數,並將誤差指定為二項分布 (binomial,即兩種可能,如T/F;Y/N)。模型參數則是先輸入應變數(y)~自變數(x)。
Call:
glm(formula = virus ~ shade, family = binomial)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.6406 -0.9993 -0.7340 1.0510 1.6990
Coefficients:
Estimate Std. Erro z value Pr(>|z|)
(Intercept) -1.5436 0.5976 -2.583 0.00979 **
shade 0.3697 0.1338 2.763 0.00573 **
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 96.983 on 69 degrees of freedom
Residual deviance: 88.442 on 68 degrees of freedom
AIC: 92.442
Number of Fisher Scoring iterations: 4
#輸出結果後,「Intercept (截距)」這行可以知道「遮陰類別為0時,病毒帶原狀況」。shade這行是擬和直線的斜率,其P遠小於0.01,代表遮陰對於植物病毒帶原機率有強烈影響。
#下一行是描述假定的誤差分布(此分布可以更改),再來是有關殘差偏差值 (deviance)的比較。如果誤差分布確實如我們所指定,則殘差偏差值應等於自由度。但在此案例中,殘差偏差值大於自由度,代表資料比預想的還要分散。再來是「AIC」,即Akaike信息量準則,這是模型擬合資料能力的指標
lgt<- glm(virus~shade, binomial)
plot(shade,fitted(lgt)) #將直線的擬合視覺化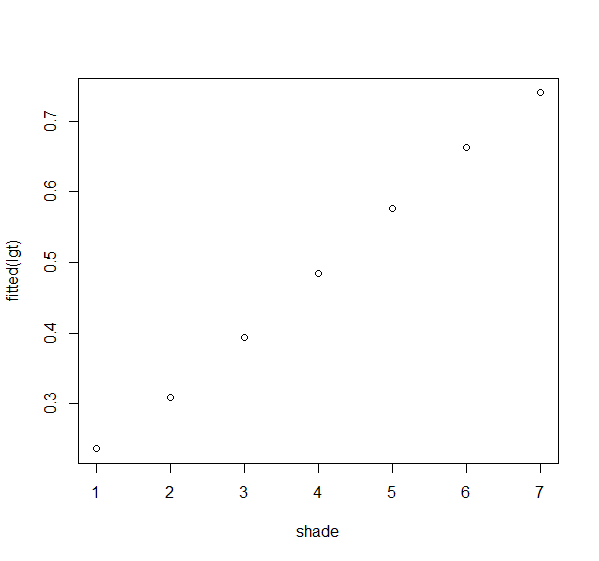
第二型模式回歸 (Model II regression)
包含一系列分析。其所作的假定遠少於第一型模式回歸。
第一型最常出問題的假定是「x 值的測量無誤差」及「對於任何 x 值,y 值的變異數均相同」,若這些假定不為真,則需使用第二型模式回歸,可惜該統計處理還在實驗階段。
Bartlett 三組檢定法是個值得推薦的第二型模式回歸,此方法把資料依 x 值大小簡單分成三組,且最大和最小這兩組的觀測數需相同。把這兩組的 x 和 y 值平均值算出後,兩個平均點之間的斜率為欲求得之斜率。
上面提到的 Kendall 最佳配適線法也是第二型模式回歸。
多項式回歸、三次回歸和二次回歸
標準回歸的其中一個假定是「x 和 y 的關係為一條直線」,但若不適用時,應少器該假定並使用多項式回歸,可以使擬合度較佳,預測更精準,缺點是要增加參數的數目,隨著擬合線越複雜,其所解釋的關係在生物學上就越沒有信服力。但還是有些方法可以判斷否值得加入新的參數,AKI 把模型擬合的精準度和使用參數的個數一起納入考量,當有許多模型可供選擇時可以協助我們做決定。
參考來源: 生物統計學:如何選擇與應用

